Quantum Chemistry
Perhaps Paul Dirac said it best when he said “The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble. “The physical law he was referring to, of course, is the Schrodinger equation, whose solutions have the potential to tell us anything we might like to know about a chemical or material of interest. The idea that with enough computational power one could predict how a molecule will behave without having to step into a lab is exciting to say the least. Unfortunately, as he alluded to, even today these equations have proven too complicated to solve exactly, and as he went on to say “It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed, which can lead to an explanation of the main features of complex atomic systems without too much computation”, which succinctly summarizes the aim of quantum chemistry today. Recently it has been suggested that Quantum Computers may offer a solution to the difficulty of this computation. I am interested not only in the use of quantum computers for this problem, but how they can better inform our classical approaches to solving this key problem.
Hybrid Quantum-Classical Algorithms
A number of algorithms for quantum computers have now been proposed that promise to greatly exceed the performance of our best known classical algorithms today. Unfortunately, the quantum resource requirements of many of these algorithms greatly exceed the current and expected near-future capabilities of quantum devices. Moreover, there are some operations and problems for which quantum computers are not known to exhibit any advantage over a classical computer. Given this and the sparse quantum resources available, it makes sense to use quantum devices only where they provide the most advantage, and offload mundane operations to a traditional computer. This is analogous to how computers today offload certain operations to accelerators that are specialized for a certain type of operation, like GPU’s. Some progress has been made in this area for quantum chemistry with the variational quantum eigensolver approach, but it raises many interesting questions about the future interplay between classical and quantum machines.
Going Beyond Low-Rank and Sparse Approximations
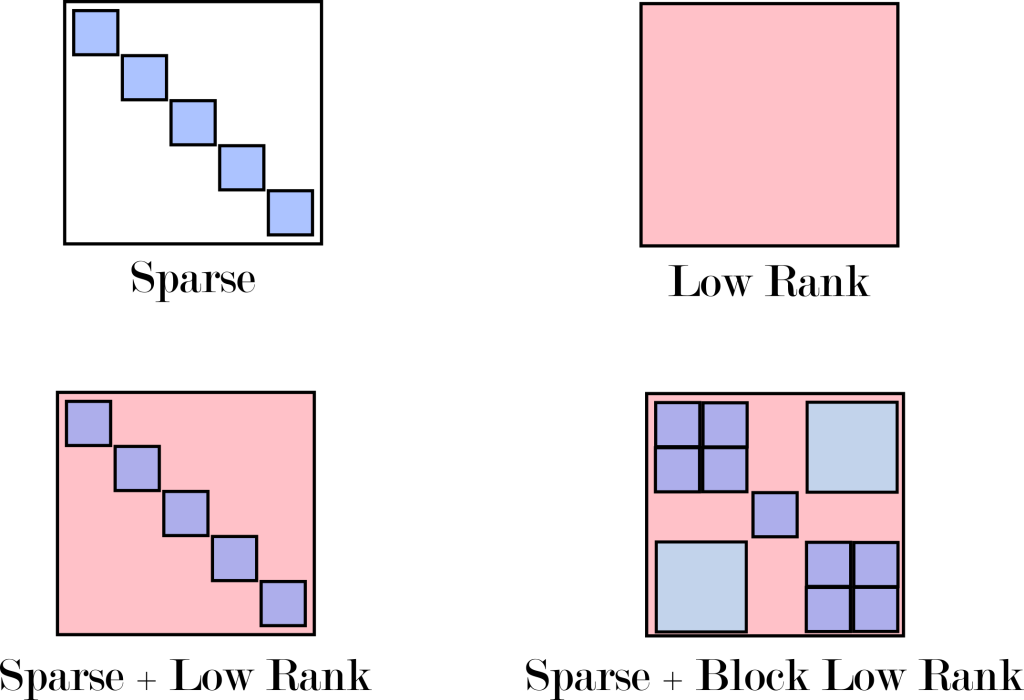 Scalable algorithms often depend on exploiting some form of simplicity in the structure of a problem. Low-rank methods and sparse methods are two examples of this type of approach, and with developments in the area of compressed sensing, we are understanding more about sparsity all the time. However, some principles are not yet as widely understood. If one considers the simple case of matrices, some matrices are sparse but not low-rank (e.g. diagonal matrices with non-zero diagonals for example), some are low-rank but not sparse (e.g. a matrix with all uniform entries), and perhaps more interestingly some are neither but still simple (e.g. the matrix arising from the discrete form of the fast multipole method). Exploiting hierarchical and recursive structure in a matrix with sparsity and low-rank as special cases is a pursuit that is arguably young compared to more traditional decompositions. Can these methods allow us to understand a more general type of information structure? Can they be extended to more general tensors in quantum mechanics for expressing correlations beyond what we think of as tensor networks today?
Scalable algorithms often depend on exploiting some form of simplicity in the structure of a problem. Low-rank methods and sparse methods are two examples of this type of approach, and with developments in the area of compressed sensing, we are understanding more about sparsity all the time. However, some principles are not yet as widely understood. If one considers the simple case of matrices, some matrices are sparse but not low-rank (e.g. diagonal matrices with non-zero diagonals for example), some are low-rank but not sparse (e.g. a matrix with all uniform entries), and perhaps more interestingly some are neither but still simple (e.g. the matrix arising from the discrete form of the fast multipole method). Exploiting hierarchical and recursive structure in a matrix with sparsity and low-rank as special cases is a pursuit that is arguably young compared to more traditional decompositions. Can these methods allow us to understand a more general type of information structure? Can they be extended to more general tensors in quantum mechanics for expressing correlations beyond what we think of as tensor networks today?
The Manifold of Physical Quantum States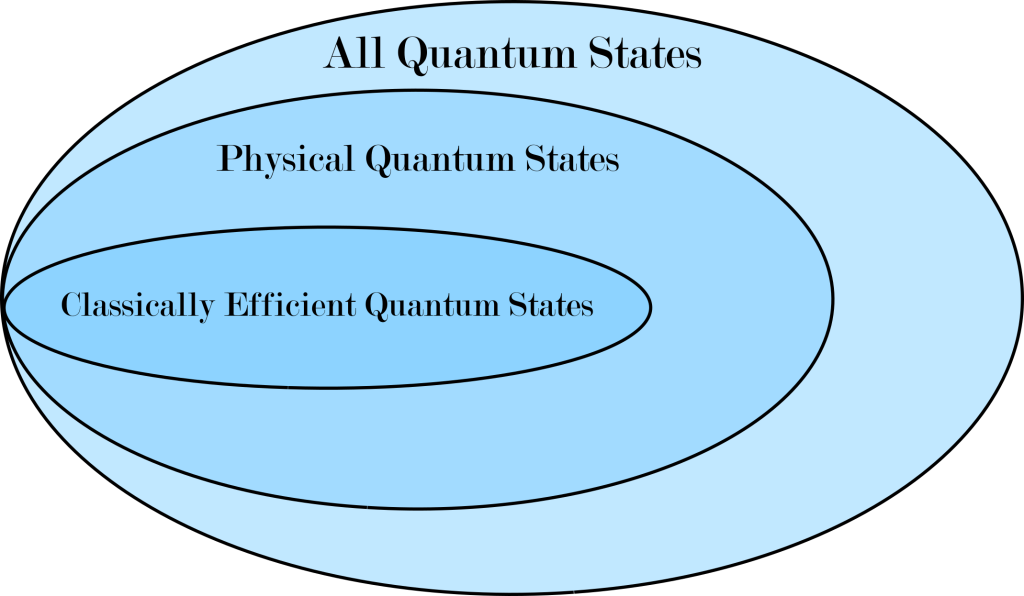
If one takes a somewhat philosophical point of view and imagines the universe as a giant quantum computer, a few questions naturally arise based on what we now know about quantum evolution. For example, in the time the universe has existed, the manifold of quantum states that could have been produced by arbitrary time-dependent physical (k-local)
Hamiltonians is exponentially small in the total space of all possible quantum states. This is sometimes called the “physical corner” of Hilbert space, or used to characterize our Hilbert space view of quantum mechanics as a “convenient illusion”. How can we characterize the quantum states that actually manifest in reality? Are the states which live in this space special in some way?