Quantifying the volumes of different types of quantum states with respect to each other is an interesting tool for analysis that I’ve recently become interested in. For example, did you know the volume of separable states is super-doubly-exponentially small with respect to all quantum states? That means that if I choose a state of 100 qubits randomly from Hilbert space, with overwhelming probability that state will be entangled. It also raises the bar for any would-be entanglement witness to beat the performance of an algorithm which guesses entangled for every state blindly if the test set is all possible quantum states. Of course, if you talk to any person working in an experimental quantum lab, they would certainly like it if almost everything they did resulted in an entangled state, unfortunately that’s not really reality, and we know that the set of physical states we expect to see is a tiny subset of all possible states. Coming up with a measure that reflects that reality and readily enables computation would be valuable indeed.
Regardless, one of the tools used in many of these analyses at the moment is integration over the unitary group. This is because the unitary group allows us a way to generate all possible quantum states from some choice of starting state. To complete these analyses one must also integration over the simplices of eigenvalues corresponding to physical states, but for now I want to focus on the unitary group. To talk about integration, we need some way of quantifying volume, or a measure. The unitary group has a natural measure, its unique Haar measure that treats all unitary operators equally. It does this by being invariant under the action of the unitary group, in the same way you wouldn’t want the volume of a box to change if you translated it through space. Mathematically we can phrase this as saying ![]() , which leads to a corresponding Haar integral with the defining property
, which leads to a corresponding Haar integral with the defining property
(1) ![]()
for any integrable function ![]() , group elements
, group elements ![]() , and the last equality is written to match the shorthand commonly found in papers. We should also note that it is convention to fix the normalization of integration over
, and the last equality is written to match the shorthand commonly found in papers. We should also note that it is convention to fix the normalization of integration over ![]() of the identity to be
of the identity to be ![]() . So that’s all very interesting, but something harder to dig up, is how to actually compute that integral for some actual function
. So that’s all very interesting, but something harder to dig up, is how to actually compute that integral for some actual function ![]() that has been given to you, or you find interesting. I’ll show a few options that I’ve come across or thought about, and if you know some more, I’d love it if you would share them with me.
that has been given to you, or you find interesting. I’ll show a few options that I’ve come across or thought about, and if you know some more, I’d love it if you would share them with me.
Integration through invariance
Some integrals over the unitary group can be done using only the invariance property of the Haar integral given above, and reasoning about what it implies. This is best illustrated through an example. Suppose that ![]() , where
, where ![]() indicates Hermitian conjugation, and the integral I am interested in is
indicates Hermitian conjugation, and the integral I am interested in is
(2) ![]()
Now take any ![]() and start using that integral invariance property as
and start using that integral invariance property as
(3) ![Rendered by QuickLaTeX.com \begin{align*} VD(X)V^{\dagger} &= V \left[ \int UXU^\dagger dU \right] V^\dagger \notag \\ &= \int (VU)X(VU)^\dagger dU \text{ (By integral linearity)} \notag \\ &= \int UXU^\dagger dU \text{ (By integral invariance)} \notag \\ &= D(X) \end{align*}](https://jarrodmcclean.com/wp-content/ql-cache/quicklatex.com-844c2ed1bf8af2fca3db5ee1c2e4e06c_l3.png)
Thus we find that ![]() for all
for all ![]() , implying that
, implying that ![]() . If a matrix is proportional to the identity, then we can characterize it completely by its trace which we then evaluate as
. If a matrix is proportional to the identity, then we can characterize it completely by its trace which we then evaluate as
(4) ![Rendered by QuickLaTeX.com \begin{align*} \text{Tr}[D(X)] &= \text{Tr} \left[ \int UXU^\dagger dU \right] \notag \\ &= \int \text{Tr} \left( UXU^\dagger \right) dU \text{ (by integral linearity)} \notag \\ &= \int \text{Tr} \left( X \right) dU \text{ (by cyclic invariance of the trace)} \notag \\ &= \text{Tr}(X) \end{align*}](https://jarrodmcclean.com/wp-content/ql-cache/quicklatex.com-17d1d11cdf024550bb17ecff30eac256_l3.png)
From these two results, we conclude that
(5) ![]()
which was evaluated entirely through the defining invariance of the integral.
Monte Carlo Numerical Integration
For some problems of interest, there is no obvious way of integrating it analytically or reaching a closed result. In order to perform a numerical integration, one could choose some parameterization and attempt integration with a quadrature, but this is both cumbersome and often runs out of steam as the dimension of the problem of interest grows. Monte Carlo integration offers a straightforward way to at least attempt these integrations for high-dimensional problems of interest, and is often less human work even for low dimensional problems. Monte Carlo integration is simple, and approximates the integral as
(6) 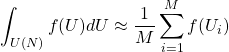
where ![]() is the number of sample points you take, and
is the number of sample points you take, and ![]() is a randomly drawn unitary that is drawn with uniform probability according to the Haar measure. How to draw unitaries uniformly with respect to the Haar measure is not entirely obvious, but luckily this has been worked out, and there are a few ways to do this. One of this requires only
is a randomly drawn unitary that is drawn with uniform probability according to the Haar measure. How to draw unitaries uniformly with respect to the Haar measure is not entirely obvious, but luckily this has been worked out, and there are a few ways to do this. One of this requires only ![]() simple steps available in most modern math libraries that are
simple steps available in most modern math libraries that are
- Fill an
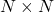 matrix with complex Gaussian IID values, call it
matrix with complex Gaussian IID values, call it 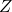 .
. - Perform a QR decomposition of the matrix
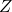 , define
, define 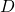 to be the diagonal of
to be the diagonal of 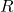 such that
such that 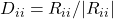 and
and 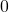 otherwise.
otherwise. - Set
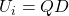 .
.
where ![]() is now the unitary of interest randomly distributed according to the Haar measure on
is now the unitary of interest randomly distributed according to the Haar measure on ![]() . Here is a Python function that can do this for you if the above steps don’t make any sense.
. Here is a Python function that can do this for you if the above steps don’t make any sense.
import numpy as np
import numpy as np
import numpy.random
import scipy as sp
import scipy.linalg
def random_unitary(N):
"""Return a Haar distributed random unitary from U(N)"""
Z = np.random.randn(N,N) + 1.0j * np.random.randn(N,N)
[Q,R] = sp.linalg.qr(Z)
D = np.diag(np.diagonal(R) / np.abs(np.diagonal(R)))
return np.dot(Q, D)
Weyl’s Integration Formula
This formula is a bit of a sledge hammer for hanging a nail, but it exists for all compact Lie groups and for the unitary group takes on the specific form
(7) 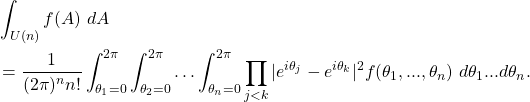
This formula also demands that ![]() be a conjugacy invariant function on the unitary group as well as symmetric in its arguments. The
be a conjugacy invariant function on the unitary group as well as symmetric in its arguments. The ![]() correspond to the possible eigenvalues that characterize all unitary matrices. I’ve yet to use it for a practical calculation, but like having a catalog of known options.
correspond to the possible eigenvalues that characterize all unitary matrices. I’ve yet to use it for a practical calculation, but like having a catalog of known options.
Elementwise Integration up to the Second Moment
Often, one is interested only in integration of some low-order moment of the Haar distribution, in which case simpler formulas exist. In particular, if the integral depends only on the ![]() ‘th power of the matrix elements of
‘th power of the matrix elements of ![]() and
and ![]() ‘th power of the matrix elements of its complex conjugate
‘th power of the matrix elements of its complex conjugate ![]() , then it suffices to consider a
, then it suffices to consider a ![]() -design. Moreover, the explicit formulas for integration take a simple form. In particular, up to the first moment we have
-design. Moreover, the explicit formulas for integration take a simple form. In particular, up to the first moment we have
(8) ![]()
which can be used to evaluate the same formula we evaluated above through invariance. That is, we seek
(9) ![]()
which we can evaluate by each element
(10) ![Rendered by QuickLaTeX.com \begin{align*} [M]_{im} &= \sum_{j,k} \int dU \ U_{ij} \rho_{jk} U_{km}^\dagger \\ &= \sum_{j,k} \rho_{jk} \int dU \ U_{ij} U_{km}^\dagger \\ &= \sum_{j,k} \rho_{jk} \int dU \ U_{ij} U^*_{mk} \\ &= \sum_{j,k} \rho_{jk} \frac{\delta_{im} \delta_{jk}}{N} \\ &= \sum_{j} \rho_{jj} \frac{\delta_{im}}{N} \\ &= \tr \rho \frac{\delta_{im}}{N} \end{align*}](https://jarrodmcclean.com/wp-content/ql-cache/quicklatex.com-3d0dea5dfc937f97cf7e531950dab428_l3.png)
using the second delta function we find the full matrix representation of ![]() is given by
is given by
(11) ![]()
which is the result we obtained above through invariance. Similarly the formula for second order can be expressed simply as
(12) 
Edit 3/20/18: Thanks to Yigit Subasi for pointing out that my Python implementation depended on the algorithm implementing the QR decomposition, and that a simple change made it independent of the method. It is now updated to reflect this fact. I also added the elementwise evaluation for integration over the Haar measure up to the second moment.