Distance measures between quantum states are interesting for all kinds of reasons. I’ve been thinking about them a lot lately as they pertain to machine learning in and around quantum mechanics, as well as just generic approaches to studying many-body quantum systems. One thing that has stuck with me lately is a peculiarity of distance between wavefunctions in many-particle quantum systems. It also seems to be intimately related with the Van Vleck catastrophe, which afflicts wavefunction based methods for studying many-body problems. In particular, almost every state seems to be equally far apart. One could call this yet another instance of the curse of dimensionality in distance functions being witnessed in all fields from quantum mechanics to more general machine learning, but for some classes of quantum states, there are other choices of distance for which such things are not true, yet they are not in common use. Let me be a bit more specific with an example
Consider a system of N qubits, or two level quantum systems with basis states ![]() and
and ![]() . A generic separable state
. A generic separable state ![]() of these qubits can be written in the form
of these qubits can be written in the form
(1) 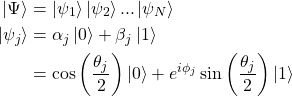
with ![]() . Without paying special attention to global phase or normalization, it’s common (perhaps because of the measurement axioms of quantum mechanics or convenience) to think of states like
. Without paying special attention to global phase or normalization, it’s common (perhaps because of the measurement axioms of quantum mechanics or convenience) to think of states like ![]() as living in the complex Hilbert space of dimension
as living in the complex Hilbert space of dimension ![]() with a natural inner product between two states
with a natural inner product between two states
(2) ![]()
A quick check of this tells you that if even a single qubit ![]() is orthogonal to qubit
is orthogonal to qubit ![]() in the primed state, the inner product is zero. If we use this inner product to define our distance metric on the total N particle Hilbert space then
in the primed state, the inner product is zero. If we use this inner product to define our distance metric on the total N particle Hilbert space then
(3) ![]()
and we see that every state ![]() which has a single qubit flipped from a state
which has a single qubit flipped from a state ![]() has a distance of 2 from that state. Recalling that this is
has a distance of 2 from that state. Recalling that this is ![]() of the possible basis states, it’s easy to see that almost every state in this space has maximal distance from every other state. Moreover, we can see that if each qubit state is only perturbed slightly such that
of the possible basis states, it’s easy to see that almost every state in this space has maximal distance from every other state. Moreover, we can see that if each qubit state is only perturbed slightly such that ![]() , we see that the squared distance between the states,
, we see that the squared distance between the states, ![]() , tends exponentially quickly towards 2 as a function of N, or a maximal distance. This can be viewed as a manifestation of the Van Vleck catastrophe for many-particle systems. While perhaps this satisfies the axioms of a distance metric, it doesn’t seem to satisfy the properties of a useful metric. Intuitively, one would like states with only a few bits different to be somehow closer than states that are totally different, or really to express some notion of similarity beyond “this is not the same state”.
, tends exponentially quickly towards 2 as a function of N, or a maximal distance. This can be viewed as a manifestation of the Van Vleck catastrophe for many-particle systems. While perhaps this satisfies the axioms of a distance metric, it doesn’t seem to satisfy the properties of a useful metric. Intuitively, one would like states with only a few bits different to be somehow closer than states that are totally different, or really to express some notion of similarity beyond “this is not the same state”.
However, if we restrict ourselves only to product states and the manifold ![]() they live on, the situation is a bit different. A product state of N qubits can be studied on the product manifold of N spheres
they live on, the situation is a bit different. A product state of N qubits can be studied on the product manifold of N spheres ![]() . Product manifolds have a natural distance derived from the sum of the distance on each of the manifolds that compose the product, and surfaces of a sphere have a natural notion of distance defined by geodesics on the sphere. Explicitly, the distance between two points on a unit sphere is given by
. Product manifolds have a natural distance derived from the sum of the distance on each of the manifolds that compose the product, and surfaces of a sphere have a natural notion of distance defined by geodesics on the sphere. Explicitly, the distance between two points on a unit sphere is given by
(4) ![]()
and the metric this induces on the manifold of the full quantum N particle state is then
(5) ![]()
which due to its form grows linearly with ![]() , and gradually increases the distance between two states as more and more of the single particle states differ. In other words it gives some meaningful notion of similarity between states.
, and gradually increases the distance between two states as more and more of the single particle states differ. In other words it gives some meaningful notion of similarity between states.
So what we see here is a case where the same quantum state, considered in Hilbert space and on its natural product manifold have two very different distances. The distance in Hilbert space is somehow related to the axioms of quantum measurement, while the distance on the manifold gives us some meaningful idea of similarity between states. This notion of meaningful distance can be extended to anti-symmetric product states as well, such as those that describe electronic systems, where the representatives are members of the Grassmann manifold (see this great paper for more information).
Unfortunately for more interesting entangled states, these notions are less straightforward to define and often the manifold geodesics don’t have closed forms. This brings me to an interesting question, which is what is the manifold of physical quantum states? What is the best notion of distance in this manifold? I’m not sure too much is known about it, but apparently it’s exponentially small in the convenient illusion of Hilbert space which is interesting in its own right…